(xi- M)2=scarto quadratico
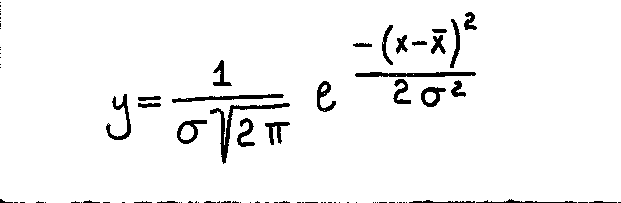
equazione di GAUSS
Se l'insieme dei dati fosse casuale ed illimitato potrebbe essere rappresentato con la curva di GAUSS,rappresentata questa curva ha questa proprietà:
s = Ö (å xi- M )2/(N-1)dove :xi- M =scarto
(xi- M)2=scarto quadratico
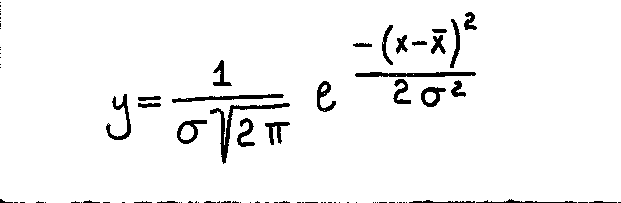
equazione di GAUSS
Se l'insieme dei dati fosse casuale ed illimitato
potrebbe essere rappresentato con la curva
di GAUSS,rappresentata questa curva ha questa proprietà:
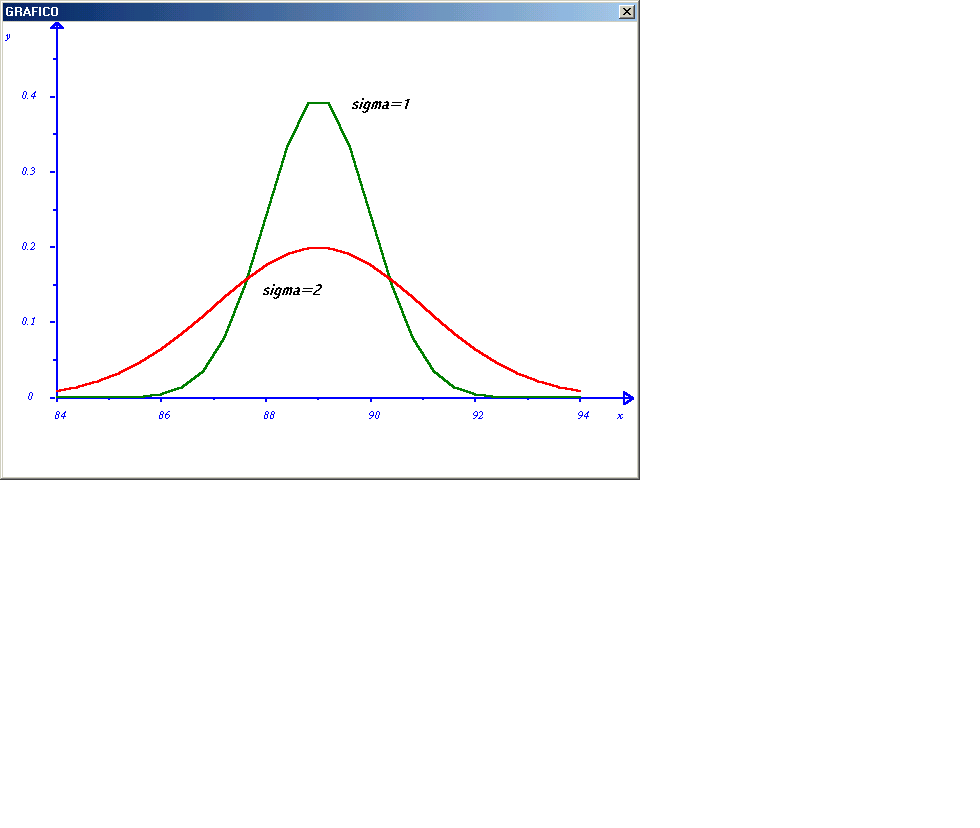
FIGURA 1
ESEMPIO DI ELABORAZIONE DATI
i dati:
89.95 89.90 89.80 89.75 89.90 90.00 89.80 89.70 89.75 89.90 89.85 90.00 89.80 89.75 89.65
L'elaborazione conil programma GAUSSIANA
:
data:19/10/2003 ora:13.43.22 file:C:\software
scuola\ZULLI.TXT
numero punti: 14 minimo 89.650 massimo 90.000
media 89.825
s =deviazione standard=0.049
punto.....valore.....scarto.... scarto .quadratico 1 89.650 -0.175 0.031 2 89.700 -0.125 0.016 3 89.750 -0.075 0.006 4 89.750 -0.075 0.006 5 89.750 -0.075 0.006 6 89.800 -0.025 0.001 7 89.800 -0.025 0.001 8 89.800 -0.025 0.001 9 89.850 0.025 0.001 10 89.900 0.075 0.006 11 89.900 0.075 0.006 12 89.900 0.075 0.006 13 90.000 0.175 0.031 14 90.000 0.175 0.031
LA RAPPRESENTAZIONE DEI DATI
L'asse x va dal valore minimo dei dati :89,65
al valore massimo=90,00,eventualmente allargando
questi estremi come in figura Il campo (90,00-89,65)
viene diviso in 50 intervalli aventi quindi
ampiezza=DX=0,0071 Per ogni intervallo: viene
riportato un rettangolo avente larghezza
=DX l'altezza è uguale a : k n , dove
n è il numero dei dati compreso nell'intervallo
. Ad esempio nell' intervallo 89,65<=<x<89,657
è compreso un solo dato(89,65).Il
valore di k è preso in modo che tutta
l'area dei rettangoli si pari a 100. Nel
caso di figura essendo il numero dei dati
14 si ha: k X 14 x 0,0071=100 e quindi k=1006
Sul grafico, figura 2 , viene riportata anche
la curva di gauss(l'area sottesa dalla curva
è anche essa=100) 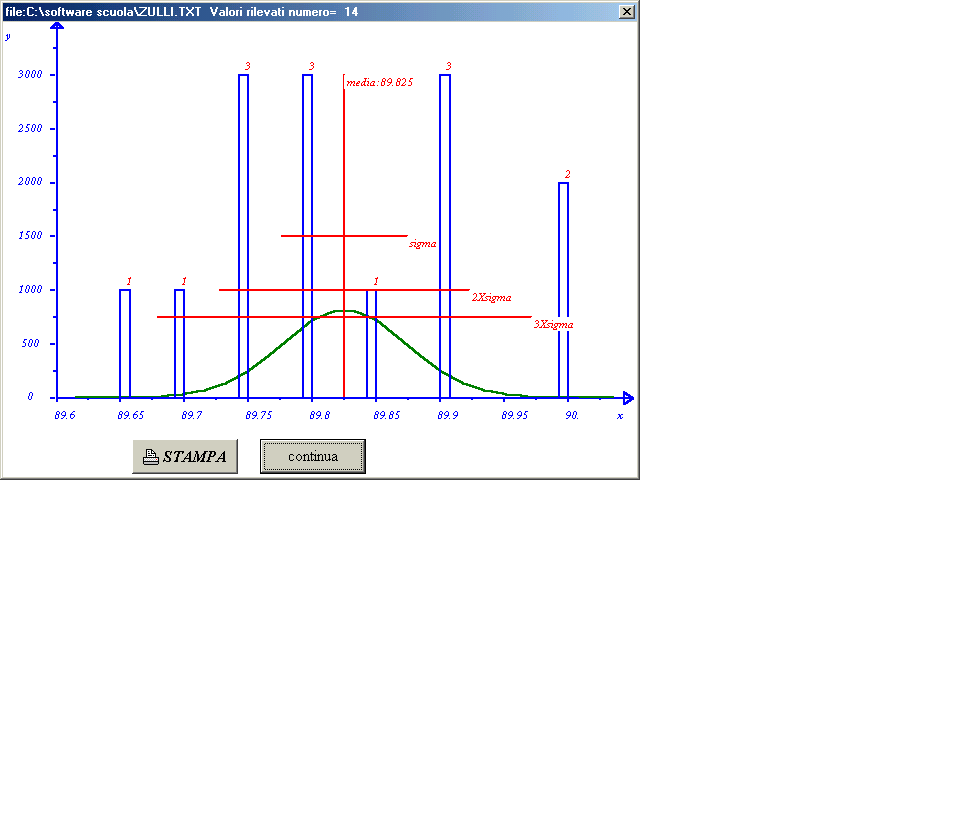 Figura 2
Figura 2  FIGURA 3 Nella figura 3 vengono riportati i grafici:
FIGURA 3 Nella figura 3 vengono riportati i grafici: