Applicazioni del freddo con il calcolo automatico

NICOLA TARASCHI

docente, libero professionista - Saronno

1. INTRODUZIONE

Il problema centrale della refrigerazione dei prodotti alimentari e’ quello di determinare il carico termico del prodotto ovvero la potenza frigorifera necessaria per raggiungere nel prodotto la temperatura richiesta ed il tempo necessario. Nell’ambiente nel quale e’ collocato il prodotto, tipicamente il magazzino frigorifero, il carico frigorifero derivante dal raffreddamento della derrata viene a sommarsi a tutti quelli derivanti, ad esempio, dalle dispersioni di calore, dal calore prodotto dalle macchine elettriche e cosi’ via. Con il metodo degli elementi finiti e’ possibile studiare l’andamento delle temperature in forme geometriche elementari (la sfera, il cilindro indefinito, la piastra indefinita), con un’ analisi semplicemente monodimensionale. Nondimeno con lo stesso metodo sarebbe possibile analizzare figure geometriche piu’ complesse in regime bidimensionale o tridimensionale. D’altra parte le condizioni reali del prodotto da refrigerare sono ben lontane da quelle del calcolo matematico. Espressioni di calcolo piu’ o meno empiriche reperibili in letteratura hanno un campo di azione ristretto. La nozione di tempo di mezzo raffreddamento mette a disposizione un dato troppo limitato per un’ indagine corretta. Nel caso di corpi conduttivi (numero di BIOT inferiore a 0,1) , la legge di raffreddamento e’ legata alla costante di tempo del corpo t :

t = M c / (h_c A)

Rilevata pertanto la curva temperatura-tempo e’ pertanto possibile ricavare, noti che siano la massa M ed il calore specifico c, il prodotto fra il coefficiente di convezione h_c e la superficie esterna A. La "conoscenza termica " del prodotto e’ quindi completa. Purtroppo i prodotti alimentari non possono essere considerati conduttivi in quanto hanno una conduttivita’ l variabile fra 0,2 e 1,2 W/(m K). In queste condizioni si verificano dei gradienti termici all’interno del corpo che differenziano le temperature interne e superficiale. L’analisi del raffreddamento [1], in un ambiente a temperatura costante, di corpi conduttivi e non conduttivi porta alle seguenti conclusioni:

• in un corpo non conduttivo la temperatura superficiale si mantiene piu’ bassa che nel corpo conduttivo
• nel corpo non conduttivo il centro termico "insegue" piu’ lentamente la temperatura esterna
• la potenza frigorifera istantanea derivante dal raffreddamento del prodotto e’ quindi minore nel corpo non conduttivo, mentre maggiore e’ il tempo di refrigerazione.
• L’energia frigorifera necessaria per ottenere nel centro termico la temperatura richiesta e’ maggiore nel corpo non conduttivo, per la presenza dei gradienti termici. Per ottenere infatti al centro termico la temperatura richiesta si avra’ nel resto della massa una temperatura inferiore.

Figura 1:il modello termico che sostituisce la massa diffusa della derrata

2-IL MODELLO TERMICO

L’analisi termica che vogliamo proporre e’ quella che sostituisce la massa diffusa della derrata con due masse concentrate M_s ed M₀, connesse da una conduttanza totale C. La massa M_s ha la temperatura superficiale t_s, mentre la massa M₀ ha la temperatura del centro termico t_o. Considerando anche il calore specifico c del prodotto, le masse M_s ed M₀ hanno capacita’ termiche complessive rispettivamente M_s c ed M₀ c. Le equazioni di equilibrio termico, in regime termico evidentemente variabile, delle due masse sono:

M_s c D t_s/D t + h_C A_p (t_s-t_a) +C (t_s-t_o) =0 (1)

M₀ c D t_o/D t - C (t_s-t_o) =0 (2)

Inoltre e’:

M_s + M₀ = M_tot (3)

dove:

• h_C A_p = il prodotto fra il coefficiente di convezione h_C e la superficie esterna del prodotto A_p
• M_tot = la massa totale del prodotto
• t_a = la temperatura dell’ambiente, che si suppone costante

• D t = l’intervallo di tempo

• D t_s = incremento temporale della temperatura superficiale

• D t₀ = incremento temporale della temperatura del centro termico

In queste equazioni 4 sono le grandezze incognite: le masse M_s, M₀ , la conduttanza C, il prodotto h_C A_p (si suppone noto il calore specifico del prodotto). Il rilievo sperimentale ad intervalli di tempo D t della temperatura superficiale e del centro termico del prodotto in un arco temporale consente di determinare i termini:

S ₁ = sommatoria dei termini D t_s/D t

S ₂ = sommatoria dei termini D t₀/D t

S ₃ = sommatoria dei termini t_s-t_o

S ₄ = sommatoria dei termini t_s-t_a

Per quanto riguarda il termine (h_c A_p ) si fa notare che si puo’ uguagliare il calore disperso dal corpo per convezione con il calore sensibile perso dalla massa del corpo:

q = h_c A_p S (t_s-t_a) D t = M_tot c (t_in-t_m) (4)

dove:

• t_in = temperatura iniziale del corpo
• t_m = temperatura media finale del corpo
• S (t_s-t_a) = sommatoria nell’arco di tempo delle differenze t_s-t_a

Rimane implicito che il rilievo della temperatura media e’ piuttosto incerto, puo’ comunque scaturire dalla media di piu’ valori in punti differenti. Noto che sia il valore della sommatoria S (t_s-t_a) D t e la temperatura media t_m si puo’ ricavare il termine h_c A_p . Ricordando inoltre che :

S (t_s-t_a)= S ₄

si ha infatti:

h_c A_p = M_tot c (t_in-t_m)/(S ₄ D t ) (5)

Nelle equazioni (1) (2) (3) rimangono pertanto solo 3 incognite che possono essere cosi’ risolte:

M_s = (-h_c A_p S ₄ - M_tot c S ₂ )/ [c (S ₁ -S ₂)]

M₀ = M_tot - M_s

C = M₀ c S ₂ / S ₃

2. 1 CONFRONTO DEL MODELLO CON LE 3 FORME ELEMENTARI

Un primo esame del modello cosi’ presentato viene fatto con le forme geometriche elementari prima presentate, di cui si dispone della soluzione che potremmo dire reale, con il metodo degli elementi finiti. Le condizioni prese in esame sono:

• conduttivita’ del corpo l = 0,5 W/(m K) (che e’ quella delle carni e del pesce)
• calore specifico= 2,093 kJ/(kg K)
• dimensione del raggio r della sfera, del cilindro, semispessore della piastra= 60 mm(la piastra viene esaminata, per la sua simmetria, per meta’ e quindi lo spessore e’ di 120 mm)
• numero di strati in cui si suddividono i corpi = 20
• intervallo di tempo di calcolo = 5 secondi
• temperatura iniziale del corpo = 25 ° C
• temperatura finale di calcolo = 2 ° C
• temperatura ambiente = 0 ° C.

La figura 2 riporta l’andamento delle temperature del centro termico e superficiale sia nel caso reale che nel caso che chiameremo teorico, che e’ quello del modello prima introdotto, ricavato cioe’ con le equazioni (1) (2) (3). Si puo’ notare che :

• vi e’ una certa differenza nel periodo di tempo iniziale fra le temperature superficiali:questa differenza finisce poi per annullarsi dopo i primi 50 minuti
• rimane verso la fine delle curve una differenza minima fra le temperature del centro termico(inferiore ad 0,5 ° C)
• Il calcolo reale da un tempo necessario per portare il centro termico a 2,5° C di 188 minuti, mentre quello teorico risulta di 205 minuti, con un errore del 9%.
• dal punto di vista complessivo la differenza fra l’energia frigorifera reale e quella teorica ( DQ% nel grafico) rimane minima(inferiore all’1%)

Nel grafico sono riportati anche i valori di:

• l
• il valore di C
• M₁ = M_s/M_tot , M₂ =M₀/M_tot
• S1 = å ₁, S2 = å ₂ , S3 = å ₃, S4 = å ₄

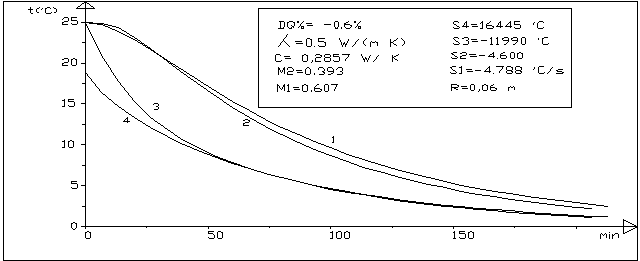
Figura 2:confronto fra le curve temperature-tempo nel caso della sfera

1-centro termico caso teorico 2-centro termico caso reale

3-superficie caso teorico 4-superficie caso reale

Queste considerazioni rimangono sostanzialmente immutate nelle altre forme :

• il cilindro indefinito, figura 3
• la piastra indefinita , figura 4

Dati reali reperiti nella letteratura tecnica [2], vengono analizzati nelle figure 5 e 6. La prima e’ riferita ad una carcassa di suino(80 kg), la seconda a quarto di bue(100 kg).

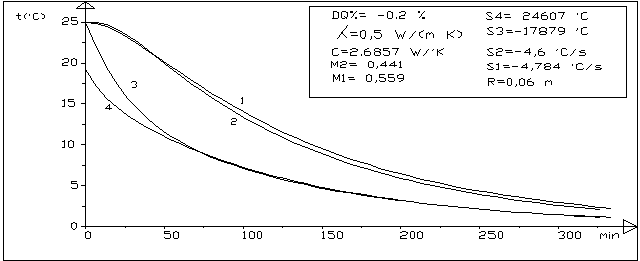
Figura 3:confronto fra le curve temperature-tempo nel caso del cilindro

1-centro termico caso teorico 2-centro termico caso reale

3-superficie caso teorico 4-superficie caso reale

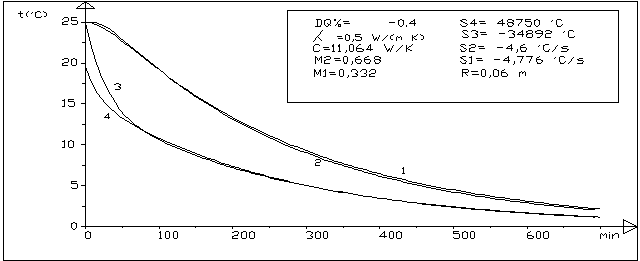
Figura 4:confronto fra le curve temperature-tempo nel caso della piastra

1-centro termico caso teorico 2-centro termico caso reale

3-superficie caso teorico 4-superficie caso reale

L’andamento delle curve teoriche segue quelle delle curve reali. Nel caso della figura 5 si riscontra il raggiungimento di 5,5° C al centro termico dopo 534 min(caso reale), e 581 minuti(caso teorico), con un errore del 9%. Dopo 10 ore si ha un errore sulla temperatura superficiale di circa 1,5 ° C ed un errore sull’energia frigorifera di circa -2,8 %. Nel caso della figura 6 l’errore sul tempo di refrigerazione( dopo 20 h) e’ praticamente nullo, l’errore sulla temperatura superficiale e’ inferiore ad 1 ° C , l’errore sull’energia di refrigerazione -2,5 %. La corrispondenza puo’ pertanto ritenersi accettabile nel caso che il modello venga introdotto per ambienti a lenta variazione di temperatura o a temperatura costante. Non puo’ essere ritenuto accettabile, per l’errore iniziale, nel caso di variazione periodica di temperatura, ma questo non rientra nei casi pratici.

2. 2 L’ANALISI DEL MODELLO TERMICO

Un’ analisi sistematica dei dati per le 3 forme viene riassunto nelle figure 7, 8, 9, 10. A dire il vero non c’e’ alcuna necessita’ di ricavare le 3 grandezze cercate nelle forme geometriche elementari, dato che si dispone della soluzione esatta, a parte il vantaggio di un tempo di calcolo piu’ ridotto. L’esame viene invece condotto per capire l’andamento qualitativo delle 3 grandezze in funzione delle dimensioni e delle grandezze termiche del corpo (conducibilita’ e calore specifico). Per quanto riguarda il calore specifico l’analisi dimostra che non vi e’ sostanziale differenza nei valori delle 3 grandezze del modello al variare del calore specifico. Nella figura 7 viene riportato il valore di M₁, in funzione della dimensione. Per quanto riguarda il significato di M₁ ed M₂ si rimanda a quanto detto nel caso della figura 2. Si noti l’incremento minimo in funzione della dimensione geometrica per tutte e 3 le forme. Sul valore della conduttanza C, figura 8, influisce la dimensione della forma in modo differenziato:

Figura 5:confronto fra le curve temperature-tempo nel caso della carcassa di suino

1-centro termico caso reale 3-superficie caso reale

2-centro termico caso teorico 4-superficie caso teorico

• nel caso della piastra questa diminuisce in modo non lineare
• nel caso del cilindro rimane costante
• nel caso della sfera aumenta in modo lineare

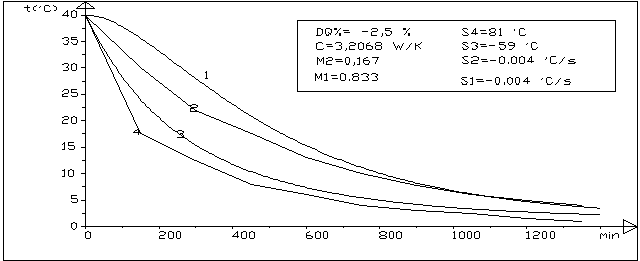
Figura 6:confronto fra le curve temperature-tempo nel caso del quarto di bue

1-centro termico caso teorico 2-centro termico caso reale

3-superficie caso teorico 4-superficie caso reale

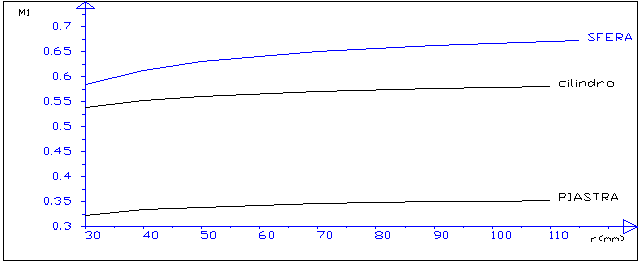
Figura 7:variazione di M₁ in funzione della dimensione

L’influenza della variazione di _l sul valore della conduttanza C e’ invece notevole , com’era logico aspettarsi, ed e’ praticamente lineare(figura 9). La figura 10, infine, visualizza la variazione sul valore di M₁ dovuta alla variazione di _l . Si puo’ vedere che la variazione e’ minima nel caso della sfera o della piastra, praticamente nulla nel caso del cilindro.

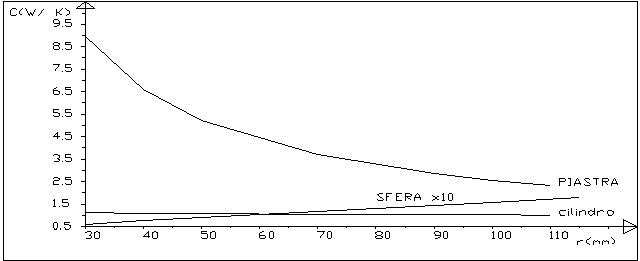
Figura 8:variazione di C in funzione della dimensione

In definitiva disponendo delle grandezze M₁, M₂, C, h_c A_p, e’ possibile calcolare il tempo di refrigerazione (dalla curva della temperatura del centro termico), ed il carico frigorifero(dalla curva della temperatura superficiale).

Figura 9:variazione di C in funzione della conducibilita’ l

3. LA SIMULAZIONE DEL COMPORTAMENTO TERMICO DEL MAGAZZINO FRIGORIFERO

Esaminiamo il comportamento termico di un magazzino frigorifero, con riferimento al modello termico prima esposto. I carichi termici sono rappresentati da:

• le dispersioni di calore q₁ attraverso la superficie esterna, esprimibili con l’espressione:

q₁=K_d A D t

dove:

K_d=trasmittanza delle pareti

A=superficie esterna disperdente del magazzino

D t=differenza di temperatura ambiente-esterno=t_a-t_est

t_est=temperatura esterna

• le dispersioni q₂ per il ricambio dell’aria , esprimibili con l’espressione:

q₂ = K_v V D t

dove:

• Kv= costante che tiene conto del calore specifico volumico dell’aria e del numero di ricambi orari
• V= volume dell’ambiente
• l’apporto termico di lampade e ventilatori pari a q₃:

Le espressioni relative a q₁ e q₂ possono essere sommate come:

q = K _G D t

dove :

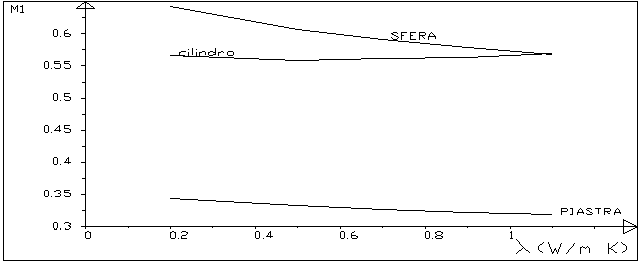
Figura 10:variazione di M₁ in funzione della conducibilita’ l

K_g = K_d A+K_v V

La potenza frigorifera fornita dal compressore sia funzione della temperatura di evaporazione t_ev del fluido frigorifero. L’equilibrio termico dell’ambiente puo’ scriversi:

Mc_a D t_a/D t +h_c A_p (t_a-t_s) +K_g(t_a-t_est)-P_frig+q₃ =0 (6)

dove:

• Mc_a =

• h_c A_p =

• t_a =

• t_s =

Supponiamo che l’apporto termico del prodotto sia relativo sia al calore sensibile che al calore latente(traspirazione del prodotto), quest’ultimo proporzionale anch’esso alla temperatura superficiale ed alla superficie del prodotto). Il rilievo sperimentale dei valori della temperatura ambiente, di quella superficiale del prodotto, della potenza frigorifera erogata, della temperatura esterna, puo’ condurre alla determinazione delle grandezze incognite che sono: Mc_a e K_g . Supponiamo, anche in questo caso, che vi sia un rilievo dei valori delle temperature in un arco di tempo. Sia allora, nell’arco di tempo considerato:

S ₅ = la somma dei valori D t_a/D t

S ₆ = la somma dei valori (t_s-t_a)

S ₇ = la somma dei valori (t_a-t_est)

S ₈ = la somma dei valori (-P_frig+q₃)

ne deriva :

Mc_a S ₅ +h_e A_p S ₆ +K_g S ₇ +S ₈ =0

Teoricamente si possono fare piu’ rilievi, tutti riconducenti alla stessa equazione. Un altro rilievo puo’ essere fatto a vuoto, senza la presenza del prodotto:

Mc_a D t_a/D t +K_g (t_a-t_est)-P_frig+q₃ =0

da cui analogamente:

Mc_a S ₉ + K_g S ₁₀ +S ₁₁ =0

La soluzione del sistema permette di ricavare le incognite. A questo punto siamo in grado di prevedere il comportamento dello stesso prodotto, nelle stesse condizioni, sia con masse differenti che con differenti temperature (ma nelle stesse condizioni di scambio termico esterno).

Esaminiamo ora il modello teorico presentato nel magazzino frigorifero in cui assumiamo i seguenti dati:

• La temperatura ambiente iniziale = 0° C
• Il compressore abbia potenza frigorifera[Watt] =16250+750 t_ev
• Coefficiente di scambio termico convettivo prodotto-ambiente h_c=12 W/(m² K)
• Capacita’ termica ambiente Mc_a pari a 3,5 volte quella del prodotto
• Il prodotto e’ costituto da 5000 sfere di raggio r pari a 60 mm con temperatura iniziale pari a 37 ° C e calore specifico 2,093 kJ/( kg K), massa volumica r = 1000 kg/m³
• ogni sfera ha pertanto capacita’ termica: 1,894 kJ/ K e massa = 0,9 kg

Le grandezze del modello termico sono:

• M_s = 0,55 kg
• M₀ = 0,35 kg
• C = 0,2857 W/ K

Nell’esempio si suppone nulli i termini: K_g (t_a-t_est) e q₃. La figura 11 riporta, in funzione del tempo, in ore:

• la temperatura teorica curva 2, calcolata con il modello, e quella reale curva 1, calcolata con il metodo degli elementi finiti, del prodotto
• la temperatura ambiente
• la potenza frigorifera P_frig in kW

Figura 11: curve della temperatura del prodotto(1 teorica, 2 reale), ambiente e della potenza frigorifera P_frig (kW)

Si noti la differenza minima fra le temperature del prodotto reale e teorica. Si noti anche l’innalzamento della temperatura ambiente come conseguenza dell’immissione del prodotto nell’ambiente.

RIFERIMENTI BIBLIOGRAFICI

[1] Nicola Taraschi :IL FREDDO :TEORIA ED APPLICAZIONI, IL FREDDO GENNAIO 2000-EDITORIALE MILLER-FREEMAN

[2] Daniel Collin :APPLICAZIONI FRIGORIFERE CASA EDITRICE TECNICHE NUOVE

email:nicolataraschi@inwind.it

VAI AL SITO TERMOINRETE