Le reti acquedottistiche e la domanda variabile
Una
rete
acquedottistica può essere schematizzata nella maniera più semplice
come in
figura 1. Un serbatoio alimenta una condotta principale da cui si
ripartiscono
più condotte secondarie che portano l’acqua alle utenze. Il dislivello
geometrico fra alimentazione e tutte le utenze sia H .Applicando il
teorema di Bernoulli , in assenza di
perdite di carico, la velocità di
uscita V= √2gH e
la portata di ciascuna utenza è Qu= V x
A . La portata complessiva nel condotto
principale è pertanto Q= N Q1 dove N è
il numero di utenze o rami secondari. Pertanto la portata erogata
complessivamente aumenta in misura direttamente proporzionale alle
utenze
collegate e la portata di ogni utenza è costante.
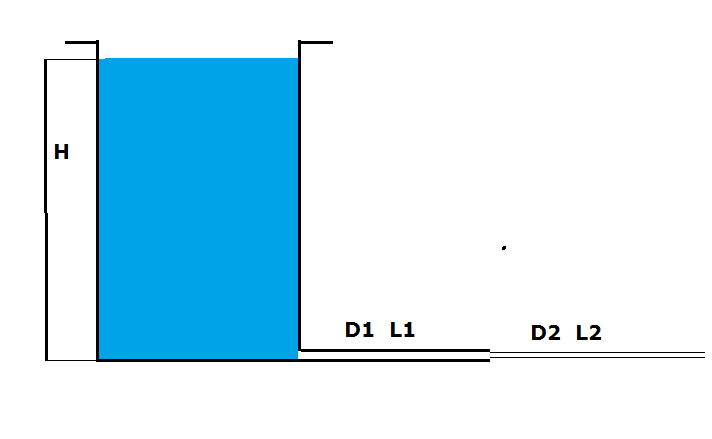
figura
1:schema della rete acquedottistica
Ben
diversa
è la situazione considerando le perdite di carico. In questo caso
riapplicando
il Teorema di Bernoulli si ha:
H-HW1-HW2=V2/2g [1]
Dove
HW1 e HW2 sono le perdite di carico della condotta principale e delle
condotta
secondaria, le quali ultime hanno le stesse caratteristiche di diametro e
lunghezza. Se supponiamo, per semplicità, che i tubi siano lisci, vale
l’equazione della perdita:
HW=k
L q1,75/D4,75
dove
K=811158641 HW in Pascal L=lunghezza in metri, q portata in m3/h
D=diametro interno in mm
Pertanto
la [1] diventa:
H-
k L1 q1,75/D14,75- k L2
(q/N) 1,75/D24,75=V2/2g [2]
Dove
q=portata della condotta principale , (q/N) portata di ognuna delle
condotte
secondarie. L1 D1 e L2 D2
rispettivamente lunghezza e diametro del condotto principale e del
condotto
secondario, v0velocità di uscita dalle condotte secondarie.
La
velocità di uscita V è a sua volta funzione della portata
, essendo
V=353
q/D2 [3]
si
ha
quindi:
V=353
q/ N D22
Pertanto:
V2/2g=3532
q2/N2 D24 2g
E
conglobando in ks=3532
/ 2g
V2/2g=Ks q2/N2 D24
In
definitiva la [2] diventa:
H- k L1 q1,75/D14,75-
k L2 q1,75/(N 1,75D24,75)-
Ks q2/N2 D24 =0 [3]
oppure:
H-
q1,75 (k L1 /D14,75- k L2
/(N 1,75D24,75)-
Ks q2/N2 D24=0
Ponendo
a=(k L1 /D14,75)
b=k
L2
/D24,75
c=Ks/ D24
si
ha in
definitiva:
H-
a q1,75 - b q1,75 /N 1,75- c q2/N2
=0
[4]
Questa
equazione può essere risolta in funzione del valore di N determinando
il valore
di q.
Un
esempio
numerico:
|
L1 |
1000 m |
|
L2 |
25 m |
|
D1 |
250 mm |
|
D2 |
50 mm |
H
25 m
|
N |
q |
q/N |
Hw1 |
Hw2 |
v |
P |
|
||
|
10 |
121,4 |
12,1 |
1,496 |
1,390 |
20,82 |
22,115 |
|
||
dove
P=pressione all’uscita dal condotto secondario
P=H-HW1-HW2 in m H2O
HW1,HW2 in m H2O
V
=velocità
uscita [m/s]
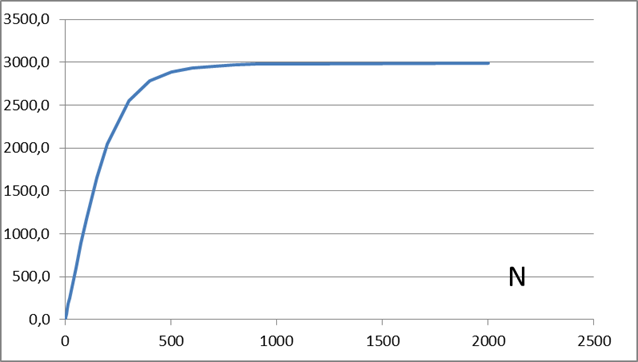
Figura
2:portata totale in funzione del numero di uenze
N
Dal
grafico di figura 2 si può notare che la portata di uscita totale
aumenta in
misura notevole fino ad un valore di N, in questo caso circa 100, per
poi
rimanere stabile sul valore massimo con un tratto orizzontale. In
questo
secondo tratto , essendo la portata totale QT costante, la portata nei
rami
secondari q1 è inversamente proporzionale al numero di utenze(figura 3):
q1=QT/N
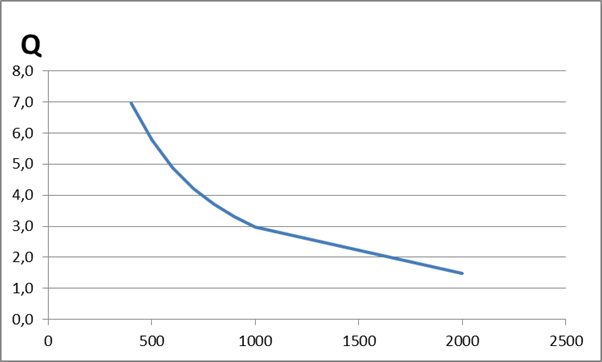
Figura 3:portata delle
utenze in
funzione del loro numero
La
portata massima è funzione del diametro del condotto principale, come
nel
grafico di figura 4
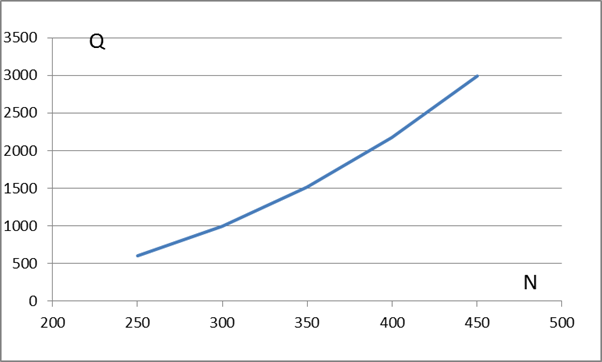
Figura
4 :portata max in funzione del diametro
del condotto
principale